Nuclear accidents: why a new quantitative scale was needed
The 2011 Fukushima-Daiichi nuclear accident has shown that the International Nuclear Event Scale (INES) is not fit for purpose. So in the summer of 2011 I designed a new, quantitative Nuclear Accident Magnitude Scale (NAMS). It was published in the online pages of Physics Today, the flagship journal of the American Institute of Physics in December 2011. Here is the link to the article, which appeared in the Points of View column, and here is a direct download as a pdf. This page is a non-technical summary.
INES was devised by the International Atomic Energy Agency (IAEA), which is essentially a trade association for promoting civil nuclear power. Deficiencies in INES have become clear in the light of comparisons between the 1986 Chernobyl and 2011 Fukushima-Daiichi accidents:
Here is a popular representation of the INES scale as a pyramid, with layers labelled 0 to 7. No 'event' can exceed the apex layer of the pyramid, level 7. Both Chernobyl and Fukushima are classed as INES level 7, whereas it is clear that Chernobyl was the more severe accident.
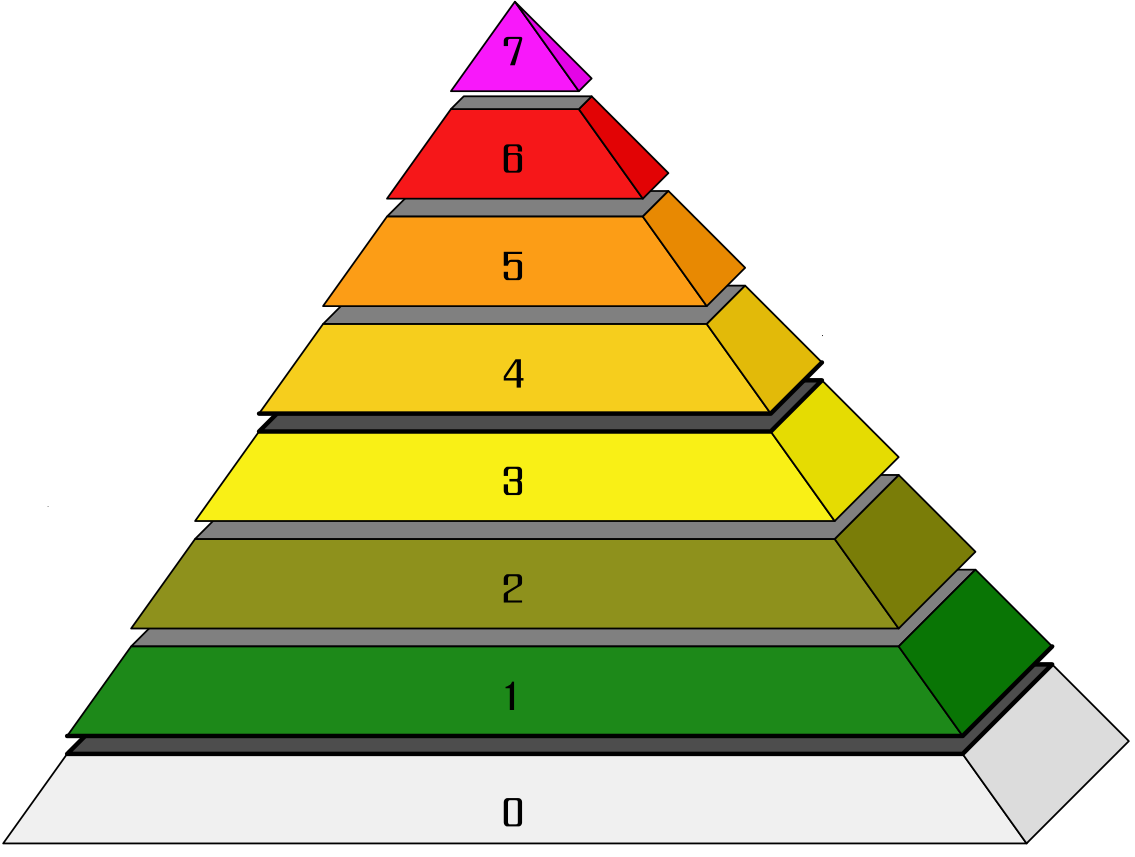
(click to toggle full-scale).
- 3: 'serious incident'
- 4: 'accident with local consequences'
- 5: 'accident with wider consequences'
- 6: 'serious accident'
- 7: 'major accident'.
The whole tenor of the document is designed to downplay and minimise the off-site effects of nuclear accidents. The words catastrophe and disaster appear nowhere. The very word 'event' is practically meaningless. The phrase 'defence in depth' is used as shorthand for 'degradation of defence in depth', which in turn is Orwellian Newspeak for failure of safety systems.
The new quantitative nuclear accident magnitude scale (NAMS) uses the earthquake magnitude approach (the so-called Richter scale) to calculate the nuclear accident magnitude M. There are 33 well-quantified accidents of the last 60 years which can be studied in detail using NAMS. It turns out that they follow a regular pattern, as with earthquakes. Put simply, bigger nuclear accidents - like earthquakes - are less common than smaller ones, and the graph of how often each magnitude occurs has a simple and elegant mathematical description. Calculation of M requires merely an estimate of the off-site escape of radioactive isotopes and what they comprise.
NAMS is a logarithmic scale, as is the earthquake magnitude scale. So one unit on the scale correponds to a factor of 10 in its size. For those who are uncomfortable with this concept the data can be presented as a simple bar chart of the amount of radioactivity released. This is shown below. I have omitted accidents with magnitude less than 2.0. The chart highlights the fact that there have been four catastrophic accidents, but provides no information on the other 21, because the bars are simply too small to show. That is why the logarithmic presentation of the same data is more meaningful.
An alternative way to show all the data more informatively is to arrange the magnitudes as a logarithmic-scale bar chart, shown below, increasing in order from the smallest to the largest magnitudes. The logarithmic vertical scale now permits the small accidents to be viewed. But the discontinuity in the spread of the data is still clear.
A frequency-magnitude distribution is a standard way to characterise earthquake patterns, but it may be too technical for some, as both variables are presented logarithmically. When applied to nuclear accidents (not shown here) we can begin to make generalisations or predictions from the data.
The magnitude measure used in NAMS is simply the logarithm of the quantity of radioactivity released to the atmosphere. The different kinds of radioactivity have been adjusted to be equivalent to Iodine-131. This is because some inhaled radioactive isotopes are much more dangerous than others. For example, Plutonium-239 is 10,000 times more damaging than Iodine-131. This is the same methodology as used in INES. There is no simple method for quantifying the health effects of marine discharges, whereby radioactive isotopes are ultimately ingested as food, therefore I have had to omit such forms of contamination from the calculation. Fortunately the ingestion of radioactivity as food is far less dangerous than breathing it in.
In contrast to earthquake magnitudes, which vary smoothly from small to large, NAMS shows that there are four exceptional nuclear accidents which are greater by 100 to 1000 times than the next largest, which has magnitude 5.2. This is shown by the step in the bar chart shown above. I was surprised to discover this, as I was expecting that the graph would show a smooth trend from frequent minor accidents to infrequent severe ones. It is highly unlikely that the gap is due to missing or unreported accidents, as they would be too big to have been suppressed or otherwise unreported.
The four catastrophic accidents are, in decreasing order of severity (where M is the NAMS magnitude):- Chernobyl, Russia 1986 (M = 8.0)
- Three Mile Island, USA (M = 7.9)
- Fukushima-Daiichi, Japan 2011 (M = 7.5)
- Kyshtym, former USSR 1957 (M = 7.3)
Unlike the INES scale, there is no upper limit to the NAMS scale. In addition, the NAMS scale comprises real numbers (with a decimal point) and not a step-like integer scale as in INES. The NAMS frequency-magnitude graph (not shown here) suggests that a catastrophic accident like one of these can be expected to occur every 12 to 15 years. The INES scale tells us that there have been only two level 7 accidents in 60 years, or about one every 30 years. So INES underestimates the frequency of such catastrophic accidents, by at least a factor of two.
Each step of 1.0 on the NAMS scale means a factor of 10 increase in severity. The gap of 2.1 between 5.2 and 7.3 therefore means a jump of approximately 10x10=100 in the amount of radioactivity released. This gap is telling us something. It suggests that perhaps there is a mechanism whereby a nuclear accident develops from small beginnings, until it gets to such a point (at somewhat over magnitude 5) that a runaway catastrophe occurs. Serious accidents at nuclear power plants have been triggered by banal events like an employee changing a light bulb, or a technician testing for air leaks with a candle and starting a major fire. Benjamin Sovacool has documented these in his book, Contesting the future of nuclear power (World Scientific, 2011).
Some may be surprised to see Three Mile Island featuring as one of the big four catastrophic accidents, with M = 7.9, given that it was only graded as INES level 5. There are two reasons for this. Firstly, the magnitude of a nuclear accident does not necessarily correlate one-to-one with its intensity, or impact, such as adverse health effects. This is comparable to earthquake magnitudes, where some of the greatest shocks have caused relatively little damage, for example because the source is very deep and/or remote from populations. Secondly, it is evident that the US federal and court systems have largely succeeded in suppressing evidence of the severity of Three Mile Island, despite good evidence to the contrary from epidemiological studies by Steve Wing and his colleagues. Their data on the elevated levels of cancer in the few years after the accident were republished as a highly telling graphic in Endeavors (the online magazine of the University of North Carolina-Chapel Hill) in 1997; In 2011 I asked for the article to be put back online, and reproduce the graphic below.
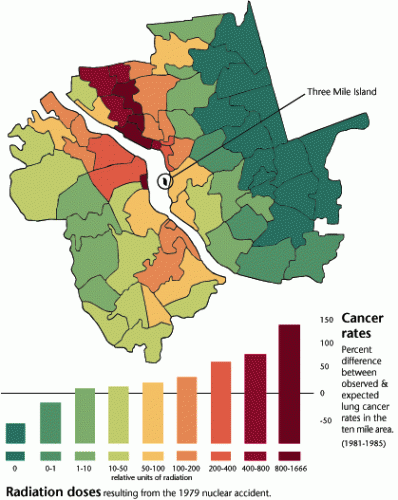
It is evident which way the wind was blowing just after the accident.
In conclusion, if the vaunted 'nuclear renaissance' does indeed come to pass, replacing the current worldwide fleet of reactors with new ones, NAMS shows that we can expect another 6 to 8 catastrophic accidents by the end of the century. Even if all the existing reactors are phased out and not replaced, there is a strong likelihood of at least two or three more Chernobyls or Fukushimas during the same period.
